Arboles

Se caracteriza por estar formado por una serie de nodos conectados por una serie de aristas.

     Hay un único nodo raíz

     Cada nodo, excepto la raíz, tiene un único padre

     Hay un único camino desde la raíz hasta cada nodo

Propiedades:

Nodo interno: nodo con algún hijo

Nodo hoja: nodo sin hijos.

Grado de un nodo: número de descendientes directos.

Grado del árbol: mayor grado de sus nodos.

Profundidad de un nodo: cantidad de predecesores.

Altura del árbol: profundidad máxima de cualquier nodo.

Camino (X, Y): sucesión de nodos que permiten llegar desde el nodo X al nodo Y.

ARBOLES BINARIOS

Es un Árbol de grado 2. Cada nodo tiene de cero a 2 descendientes directos: el hijo izquierdo y el hijo derecho.
   

è Árbol Completo: todo nodo interno tiene 2 descendientes.
   

Propiedades

nº nodos hoja <= 2^(altura del árbol)

altura del árbol <= nº nodos internos <= 2^(altura del árbol) - 1

nº nodos hoja = nº nodos internos + 1 ß árbol completo

nº nodos hoja >= altura del árbol + 1 ß árbol completo

Recorridos en profundidad de un Árbol Binario:
   

      IN-ORDEN: Se visita el subárbol izquierdo, luego el nodo y el subárbol derecho.

      PRE-ORDEN: Se visita el nodo, luego el subárbol izquierdo y el subárbol derecho.

      POST-ORDEN: Se visita el subárbol izquierdo, el subárbol derecho y finalmente el nodo.

ARBOLES BINARIOS DE BUSQUEDA (ABB)

v  El subárbol izquierdo de cada nodo es el árbol vacío o es un subárbol que contiene nodos cuya clave es menor que la suya.

v  El subárbol derecho de cada nodo es el árbol vacío o es un subárbol que contiene nodos cuya clave es mayor que la suya.

   

è Un ABB recorrido en in-orden permite obtener una lista ordenada de sus nodos.
   

Operaciones: Inserción, Búsqueda y Borrado.
   

è Equilibrio perfecto: Para cada nodo, el número de nodos del subárbol izquierdo y el del subárbol derecho difieren como máximo en 1 unidad.
   

ARBOL AVL

ABB equilibrado en altura. Para cada uno de sus nodos, las alturas de sus subárboles izquierdo y derecho difieren como máximo en 1 unidad.

ARBOLES MULTICAMINO. B, B+, B*

Son aquellos cuyo grado es mayor o igual que 2.

Formas de implementación:
  

ü  Diseñando los hijos como arrays de punteros

ü  Diseñando los hijos con punteros al hermano siguiente y a su hijo.
   

ARBOLES B

Son árboles multicamino de un orden determinado.
   

      Cada página tiene como máximo N nodos (orden del árbol).

      Cada página (excepto la raíz) tiene como mínimo N/2 nodos.

      Cada página es una página hoja o cumple que descendientes = nodos + 1.

      Todas las páginas hoja se encuentran al mismo nivel.

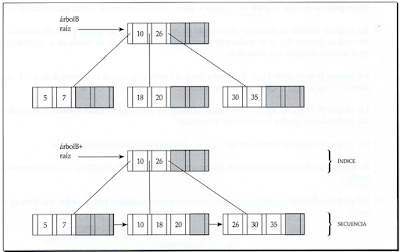
ARBOLES B+

Tienen las mismas características que los Árboles B, pero están formados por dos 2 partes.
   

Ø  Índice: nodos interiores.

Ø  Secuencia: páginas hoja enlazadas secuencialmente en las que se repiten las claves interiores.

ARBOLES B*

Árbol B especial que asegura una ocupación del 66%. Cambia el mecanismo de división y fusión de páginas.